“Toán học chỉ tiết lộ những bí mật
của mình cho những ai tìm đến bằng tình yêu thuần khiết vì vẻ đẹp của nó
mà thôi.” - Nhà toán học Des MacHale
Trên thực tế, từ thế kỷ thứ 5 trước công nguyên, toán học đã được ứng dụng trong mỹ thuật. Chính điêu khắc gia người Hy Lạp Polykleitos ở thời kỳ Hy Lạp cổ điển đã biết cách áp dụng tỉ lệ toán 1:√2 cho những tác phẩm điêu khắc cơ thể người của mình.
 Một trong những tác phẩm điêu khắc nổi tiếng của Polykleitos là tượng “người đeo vòng nguyệt quế” khắc hoạ cân đối và hoàn hảo tỷ lệ cơ thể người. Ảnh: Toplist
Một trong những tác phẩm điêu khắc nổi tiếng của Polykleitos là tượng “người đeo vòng nguyệt quế” khắc hoạ cân đối và hoàn hảo tỷ lệ cơ thể người. Ảnh: Toplist
Sau
đó, nhiều tác phẩm nổi tiếng ra đời dựa trên toán học như bức hoạ nàng
Mona Lisa của Leonardo Da Vinci. Leonardo từng là nhà toán học nên ông
hiểu rõ khái niệm về tỷ lệ vàng. Ông thu thập nhiều số liệu về tỷ lệ cơ
thể người để chọn ra tỷ lệ ông cho là cân đối nhất, tiếp đó ông mới phác
hoạ từng bộ phận theo tỷ lệ thuận với tổng thể người. Vì vậy, trong tác
phẩm, khuôn mặt của nàng Mona Lisa được vẽ cân xứng theo khuôn hình chữ
nhật có tỷ lệ vàng và tỷ lệ cơ thể nàng từ khuỷu tay bên trái đến bên
phải tạo thành tam giác tỷ lệ vàng, dựng nên tổng thể chân dung nàng
Mona Lisa hoàn hảo. Thật chẳng thổi phồng khi nói các tác phẩm nghệ
thuật này được lên ngôi một phần đều nhờ vào các khái niệm toán học đã
vận dụng trong tác phẩm.
Thế giới nghệ thuật nằm trong toán học của M.C. Escher
Toán học hay nghệ thuật đều là kết tinh của những ý tưởng sáng tạo.
Để làm chủ các con số, bạn luôn cần một bộ óc sáng tạo với trí tưởng
tượng phong phú để chắp nối những khái niệm toán học phù hợp với phạm
trù nghệ thuật mà bạn theo đuổi. M.C. Escher, nghệ nhân người Hà Lan
chính là cái tên nên được đề cử cho tài chắp nối hai lĩnh vực này khi
các tác phẩm nghệ thuật của ông đều được chi phối bởi toán học, nhờ thế
mà sở hữu nét tinh tế, thần bí và trở thành độc nhất vô nhị.
Tuy Escher chưa từng được học toán theo hệ thống giáo dục chính quy
nào, nhưng ông có niềm hứng thú với các khái niệm toán học xoay quanh
khía cạnh nghệ thuật trực quan và dành hàng giờ để quan sát. Các tác
phẩm của ông thường mang tính đặc trưng hoặc hoàn toàn dựa trên nền tảng
khái niệm toán học, kết hợp cùng tài năng nghệ thuật của mình để khiến
chúng trở thành tác phẩm nghệ thuật mang “chất Escher” riêng biệt. Chính
vì điều này mà không ít nhà khoa học trên khắp thế giới yêu quý tác
phẩm của ông. Tiêu biểu là tác phẩm “Relativity” ở năm 1951 phác hoạ một
kiểu cầu thang dài đã gây hứng thú lớn đến giới khoa học lúc bấy
giờ.
 Tác phẩm “Relativity”, M.C. Escher (1953). Ảnh: Medium
Tác phẩm “Relativity”, M.C. Escher (1953). Ảnh: MediumTuy
“Relativity” được phác hoạ tỉ mỉ, không lỗi sai sót nhưng thiếu tính
thực tế. Song, tác phẩm này đã gợi được mối quan tâm đặc biệt đến giáo
sư toán học và vũ trũ học, Sir Roger Penrose. Ông cùng cha mình thực
hiện một bài luận văn nghiên cứu chi tiết về các dạng hình học phi thực
tế và đặt tên bài luận là “Impossible Objects: A Special Type of Visual Illusion.” Bài luận văn cũng phân tích chi tiết về tam giác Penrose và “cầu thang bất tận” Penrose nổi tiếng.
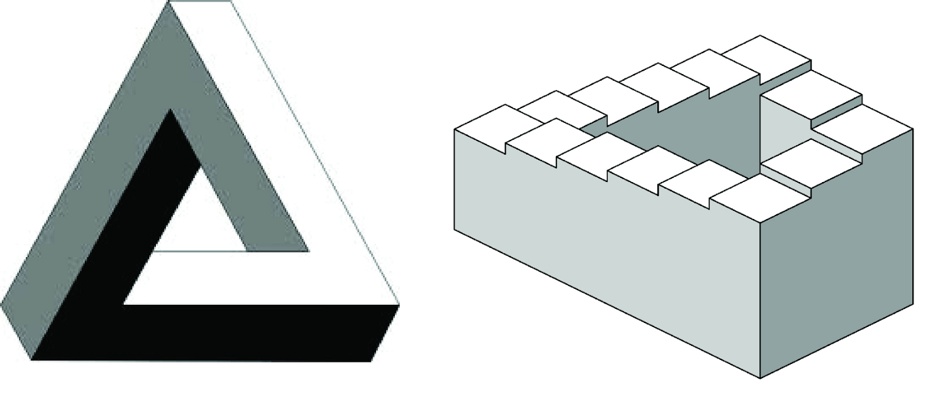 Tam giác và cầu thang Penrose. Ảnh: Medium
Tam giác và cầu thang Penrose. Ảnh: Medium
Bởi
Escher chính là nguồn cảm hứng khởi đầu cho bài viết nên Pensore đã gửi
một bản đến cho ông. Nhờ vào bài nghiên cứu chi tiết này của Pensore,
thế giới quan trong các tác phẩm của Escher đã được lột xác. Tác phẩm
sau này của ông như “Waterwall” hay “Ascending and Descending” đều chứa
đựng ý tưởng tam giác và cầu thang Penrose, nhưng trình bày theo phong
cách riêng biệt của mình.
 Ascending and Descending (1960). Ảnh: Medium
Ascending and Descending (1960). Ảnh: Medium Waterfall (1961). Ảnh: Medium
Waterfall (1961). Ảnh: Medium
Minh
chứng tiếp nối cho những tác phẩm chịu ảnh hưởng toán học ngày càng
mạnh mẽ của ông thì phải nói đến bộ tác phẩm “Regular Divisions of the
Plane”. Với những tác phẩm này, ông chọn cách pha trộn “chất” nghệ thuật
đặc trưng của mình cùng phương pháp toán học Tessellation cơ bản (là
phương pháp sắp xếp các hình (thường là hình đa giác) một cách liền kề
và không chồng lên nhau theo một trật tự lặp lại nhất định. Nhấp vào đây để tìm hiểu thêm về kỹ thuật này). Do đó,
hình vẽ nhân vật độc đáo trong bộ tác phẩm được sắp xếp cân đối, chuẩn
xác với nhau và “Circle Limit IV” là tác phẩm cuối cùng trong bộ sưu tập
phác hoạ này của ông, áp dụng phương pháp Tessellation cùng với quy tắc
phối cảnh nhằm tạo hiệu ứng giống không gian 3 chiều.
 Circle Limit IV (1960). Ảnh: Medium
Circle Limit IV (1960). Ảnh: MediumChỉ dựa vào mỗi phương pháp Tesselation thì có lẽ “Circle Limit IV”
vẫn chưa thể mang tiếng vang xa như trên thực tế. Bí thuật ở đây một
phần là nhờ vào cách vận dụng khái niệm toán học trong hình học, phép
đối xứng và cách sắp xếp để tạo cảm giác đánh lừa thị giác theo chiều
sâu trên mặt phẳng Hyperbolic, khiến nghệ thuật thăng hoa, làm mãn nhãn
người xem.
Nhờ
sự kết hợp học thức sâu rộng về toán học của Penrose và tài năng nghệ
thuật của Escher mà những tác phẩm kiến trúc đặc sắc của ông có thể ứng
dụng vào đời thực và khái niệm toán học của Penrose phần nào trở nên dễ
hiểu hơn thông qua các kiệt tác này. Ông áp dụng toán học làm bước đệm
cho công trình kiến tạo các tác phẩm nghệ thuật thành công của mình và
biến nghệ thuật trực quan thành con đường tắt đi vào thế giới toán học.
Học và thực hành toán cao cấp cùng nghệ nhân Albrecht Durer
Nghệ nhân người Đức, Albrecht Durer ở thời kỳ Phục Hưng nổi tiếng với
độ tỉ mỉ trong tác phẩm và ông chứng minh nghệ thuật ấy tất thảy đều
toát ra từ vẻ đẹp của toán học.
 Man Drawing a Lute (The Draughtsman of the Lute) (1525), Ảnh: Medium
Man Drawing a Lute (The Draughtsman of the Lute) (1525), Ảnh: Medium
Trong cuốn sách “Four Books on Measurement” (Tạm dịch: Bốn tựa sách về đo lường) do Albercht Durer viết, ông đã vẽ bức tranh minh hoạ mang tên “Man Drawing a Lute”, hướng
dẫn cách vẻ đàn luýt hoàn toàn dựa trên lý thuyết toán học. Trong bức
tranh, dụng cụ mà người đàn ông trên phải đang sử dụng chính là dụng cụ
hỗ trợ phối cảnh (Perspective machine). Ông buộc căng sợi dây
xuyên qua dụng cụ hỗ trợ vào một điểm trên cây đàn và điểm còn lại là
trên bức tường phía sau khung hình. Tại điểm sợi dây xuyên qua khung
hình, chấm một điểm lên tờ giấy ở cánh cửa nhỏ được gắn vào khung hình.
Tiếp tục lặp lại các bước như trên với các điểm khác nhau trên vật thể.
Cuối cùng, ta sẽ có được bản phác thảo cây đàn sơ bộ với chất lượng phối
cảnh hài hoà.
Nguyên lý sử dụng dụng cụ hỗ trợ phối cảnh dựa trên khái niệm toán
học về đại số tuyến tính miêu tả sự thay đổi về điểm và đường thẳng
trong không gian đa chiều (Đại số tuyến tính nghiên cứu về ước lượng các điểm và đường thẳng của không gian 3 chiều trên không gian 2 chiều).
Và đối với nhiều người không giỏi về toán cao cấp, cách diễn giải lý
thuyết qua tác phẩm minh hoạ như vừa rồi khiến mọi khúc mắc dễ được tháo
gỡ hơn.
Toán học có “hồn” nghệ nhân?
Khẳng định rằng toán học luôn là bước cơ bản để chuyển hoá nghệ thuật
vào trang giấy hay qua máy móc bởi để phác hoạ một tác phẩm, ta cần
phải hiểu nguyên tắc và logic trong toán học để giải mã nghệ
thuật. Trong thời đại số như ngày nay, máy tính trở thành vật tuỳ thân
của mỗi người. Thay vì bút nghiên giấy mực, nghệ thuật “tiến hoá”, đi
đôi cùng máy tính thời thượng và máy tính có thể tạo ra nghệ thuật, dựa
trên những quy trình toán học phức tạp ẩn trong bộ máy.
Harold
Cohen, nghệ nhân và là nhà khoa học máy tính người Anh sáng chế chương
trình sáng tạo nghệ thuật sử dụng trí thông minh nhân tạo, AARON với
mong muốn tìm hiểu điều gì quyết định một tác phẩm có nghệ thuật. Lúc
ấy, Cohen lập trình thuật toán vào chương trình và lấy những tác phẩm
nghệ thuật kinh điển làm ví dụ cho AARON. AARON sử dụng tất cả những
phép tính được lập trình, từ đó hình thành quyết định chấm từng điểm lên
mỗi vị trí nhất định trên màn hình. Cứ thế, nó lặp đi lặp lại quy trình
mà không có sự chen ngang bởi Cohen và tất cả phác hoạ của chương trình
AARON chưa bao giờ bị trùng ý tưởng.
 Theo (1992), tác phẩm chân dung kỳ quái, sắc nét của AARON thể hiện gương mặt người đàn ông đang lo âu, buồn bực. Ảnh: Medium
Theo (1992), tác phẩm chân dung kỳ quái, sắc nét của AARON thể hiện gương mặt người đàn ông đang lo âu, buồn bực. Ảnh: Medium
“Theo”,
một trong những tác phẩm của AARON, được vẽ theo thuật toán máy tính,
nhưng bị đánh giá là một tác phẩm nghệ thuật vô hồn - không ý nghĩa và
khát vọng vì người nghệ sĩ vẽ nó không thể cảm nhận cảm xúc hay có nhận
thức về chuyển động của mình. Song, nếu nhìn trên khía cạnh là một bức
tranh vẽ, “Theo” là một tác phẩm nghệ thuật bởi nó lột tả được cảm xúc
bức bối hiện trên khuôn mặt cuả người đàn ông và nhuộm bức chân dung
trong gam màu sáng bắt mắt. Những nhân tố toán học giúp khắc hoạ chân
dung khiến AARON được mệnh danh là nghệ nhân. Vậy nhìn chung, vì nghệ
thuật là huyền huyễn, là linh hồn, thế nên ta cần chuyển hoá nó bởi toán
học để “thổi hồn” vào tác phẩm. Nói cách khác, một tác phẩm luôn cần
đến “bàn tay” đắc lực của thuật toán để tạo nên tuyệt tác.
Nhận định như vậy không có nghĩa ta đang xem nhẹ nghệ thuật. Mặt
khác, nghệ thuật minh hoạ khái niệm toán học trở nên dễ hiểu và “mặn
mòi” hơn. Mấy ai có thể đoán ra những dạng hình học hiếm gặp hay phép
đối xứng trong phân dạng? (vật thể hình học có thể chia ra thành nhiều mảnh nhỏ có kích thước đồng dạng (hoặc gần như đồng dạng) với toàn thể hình).
Nhưng bằng cách mô phỏng qua hình ảnh, những nhà nghiên cứu toán học có
thể nhanh chóng tìm lời giải đáp cho các bài toán ẩn. Cũng như câu nói
của Charles Bukowski: “Người tri thức nói điều đơn giản theo cách phức tạp. Người nghệ sĩ nói điều phức tạp theo cách đơn giản.”
Kết
Chúng ta từng nghe nói những cụm từ như “tự do trong nghệ thuật” hay
“phóng túng trong nghệ thuật”, tức gạt bỏ nguyên tắc để thoả trí thể
hiện nghệ thuật. Tuy nhiên, nếu một nghệ nhân thiếu kiến thức về các
nguyên tắc và giới hạn trong toán học, anh ta có thể sẽ vật lộn với ý
tưởng để rồi nhận ra ý tưởng ấy không theo sát thực tiễn và tác phẩm
“Relativity” của Escher là một ví dụ, cùng như bài học rút ra cho chúng
ta. Thay vì nhận định toán học là thước đo giới hạn của nghệ thuật hay
là yêu sách, đòi hỏi nghệ thuật nghiêm túc tuân thủ, giới hạn toán học
không mang bất lợi nhưng cho chúng ta thấy vùng đất ngút ngàn của những
điều khả dĩ.
Người dịch: Jane
Nguồn: Medium
POLYRT - TRAINING ART DESIGN